Formulas
1.Trigonometry:
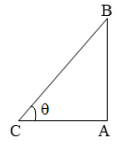
In a right angled $\triangle$OAB, where $\angle$BOA = $\theta $,
i. sin$\theta =\dfrac{Perpendicular}{Hypotenuse}=\dfrac{AB}
{OB}$
ii. cos$\theta =\dfrac{Base}{Hypotenuse}=\dfrac{OA}{OB}$
iii. tan$\theta =\dfrac{Perpendicular}{Base}=\dfrac{AB}{OA}$
iv. cosec$\theta =\dfrac{1}{sin\theta}=\dfrac{OB}{AB}$
v. sec$\theta =\dfrac{1}{cos\theta}=\dfrac{OB}{OA}$
vi. cot$\theta =\dfrac{1}{tan\theta}=\dfrac{OA}{AB}$
2.Trigonometric Formulas:
Degrees to Radians and vice versa:
360°=2π radian
Trigonometry Quotient Formulas:
tanθ=$\dfrac{sinθ}{cosθ}$
cotθ=$\dfrac{cosθ}{sinθ}$
Trigonometry - Reciprocal Formulas :
cscθ=$\dfrac{1}{sinθ}$
secθ=$\dfrac{1}{cosθ}$
cotθ=$\dfrac{1}{tanθ}$
Trigonometry - Pythagorean Formulas :
i. sin2$\theta$ + cos2$\theta$ = 1.
ii. sec2$\theta$ - tan2$\theta$ = 1.
iii.csc2$\theta$ - cot2$\theta$ = 1.
iv.1 + tan2$\theta$ = sec2$\theta$ .
v.1 + cot2$\theta$ = cosec2$\theta
$.
3.Values of T-ratios:
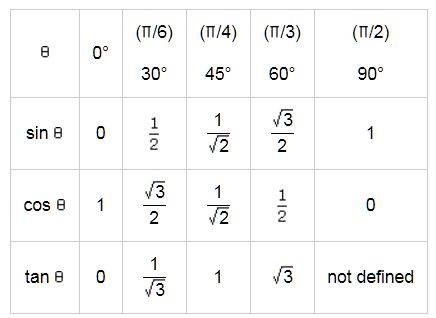
4. Important Values to memorise :
√2=1.414
√3=1.732
√5=2.236
Height and Distance :
It is an important application of trigonometry which helps us to find the height of any object and distance of that object from any point which are not directly measurable. If the angle of elevation/depression from a point is known.
In a right angled $\triangle$OAB, where $\angle$BOA = $\theta$,
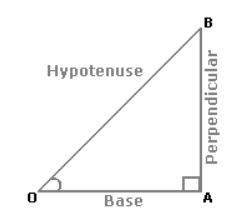
i. sin$\theta =\dfrac{Perpendicular}{Hypotenuse}=\dfrac{AB}{OB}$
ii. cos$\theta =\dfrac{Base}{Hypotenuse}=\dfrac{OA}{OB}$
iii. tan$\theta =\dfrac{Perpendicular}{Base}=\dfrac{AB}{OA}$
iv. cosec$\theta =\dfrac{1}{sin\theta}=\dfrac{OB}{AB}$
v. sec$\theta =\dfrac{1}{cos\theta}=\dfrac{OB}{OA}$
vi. cot$\theta =\dfrac{1}{tan\theta}=\dfrac{OA}{AB}$
Solved Examples - Easy
Example 1:
A balloon is connected to a meteorological station by a cable of length 200 m, inclined at 60º to the horizontal. Find the height of the balloon from the ground. Assume that there is no slack in the cable.Sol.
Let B be the balloon and AB be the vertical height. Let C be the meteorological station and CB be the cable.
Then, BC = 200 m and ∠ACB = 60ºThen,$\dfrac{AB}{BC}=sin60º=\dfrac{\sqrt{3}}{2}$
=> $\dfrac{AB}{200}=\dfrac{\sqrt{3}}{2}$
=>AB=$\left( \dfrac{200 \sqrt{3}}{2}\right)$m=173.2m
Example 2:
A 80 m long ladder is leaning on a wall. If the ladder makes an angle of 45 degrees with the ground, find the distance of the ladder from the wall.Sol.
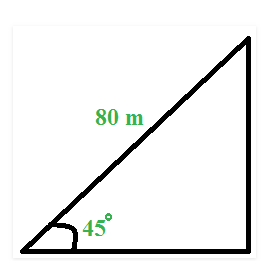Here, cos θ = Base / Hypotenuse=> cos 45º = Base / 80
=> Base = 80 cos 45 = 80 /$ \sqrt{2}$ = 40 $\sqrt{2}$
=> Distance of the ladder from the wall = 40 $ \sqrt{2}$ m
Example 3:
If a vertical pole 6m high has a shadow of length 2 √3 metres, find the angle of elevation of the sun.Sol.
Let AB be the vertical pole and AC be its shadow.
Let the angle of elevation be θ. Then,AB = 6 m, AC = 2 √3 m
and ∠ACB = θ.
Now,tan θ=$\dfrac{AB}{AC}=\dfrac{6}{2\sqrt{3}}=\sqrt{3}$=tan60º
$\therefore$ θ=60º
Example 4:
A ladder against a vertical wall makes an angle of 45º with the ground. The foot of the ladder is 3m from the wall. Find the length of the ladder.Sol.
Let AB be the wall and CB, the ladder.
Then, AC = 3m and ∠ACB = 45ºNow,$\dfrac{CB}{AC}$=sec45º= √2
=>$\dfrac{CB}{3}$=√2
∴ Length of the ladder = CB = 3 √2
= (3 × 1.41) m = 4.23 m
Example 5:
The pilot of a helicopter, at an altitude of 1200m nds that the two ships are sailing towards it in the same direction. The angle of depression of the ships as observed from the helicopter are 60º and 45º respectively. Find the distance between the two ships.Sol.
Let B the position of the helicopter and let C, D be the ships. Let AB be the vertical height.
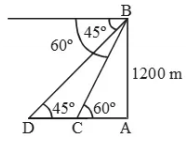Then, AB = 1200 m,∠ACB = 60º and ∠ADB = 45º.
Then,$\dfrac{AD}{AB}$=cot 45º=1
=>$\dfrac{AD}{1200}$=1
=>AD=1200
And,
$\dfrac{AC}{AB}$=cot 60º=$\dfrac{1}{\sqrt{3}}$
=>$\dfrac{AC}{1200}=\dfrac{1}{\sqrt{3}}$
=>AC=$\dfrac{1200}{\sqrt{3}}$=$400\sqrt{3}$m
Angle of Elevation:
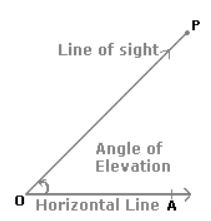
Suppose a man from a point O looks up at an object P, placed above the level of his eye. Then, the angle which the line of sight makes with the horizontal through O, is called the angle of elevation of P as seen from O.
$\therefore$ Angle of elevation of P from O = $\angle$AOP.
Solved Examples - Easy
Find the angle of elevation of the plane from point A on the ground.
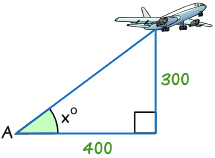
Step 1: The two sides we know are Opposite (300) and Adjacent (400).
Step 2: SOHCAHTOA tells us we must use Tangent.
Step 3: Calculate Opposite/Adjacent = 300/400 = 0.75
Step 4: Find the angle from your calculator using tan-1
Tan x° = opposite/adjacent = 300/400 = 0.75
tan-1 of 0.75 = 36.9° (correct to 1 decimal place)
Angle of Depression:
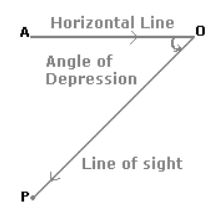
Suppose a man from a point O looks down at an object P, placed below the level of his eye, then the angle which the line of sight makes with the horizontal through O, is called the angle of depression of P as seen from O.
Solved Examples - Easy
A person in a control tower is looking down at an airplane on the runaway that is 78 yards away from the base of the tower.If this tower is 27 yards high, find the angle of depression from the tower to the airplane below.
Its a perfect rectangle thus according to the definition of tan
tanθ=$\dfrac{oppositeside}{adjacentside}$
tanθ=$\dfrac{27}{78}$
θ=tan-1$\dfrac{27}{78}$=18.77
Angle Bisector Theorem :
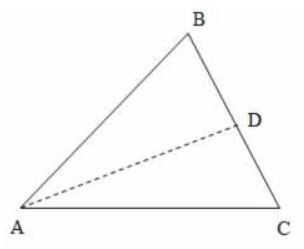
Consider a triangle ABC as shown above. Let the angle bisector of angle A intersect side BC at a point D. Then
$\dfrac{BD}{DC}=\dfrac{AB}{AC}$
(Note that an angle bisector divides the angle into two angles with equal measures.
i.e., $\angle$BAD = $\angle$CAD in the above diagram)